我的校招记录：校招笔记（零）_写在前面 ，以下是校招笔记总目录。

备注
算法能力（“刷题”） 这部分就是耗时间多练习，Leetcode-Top100 是很好的选择。 补充练习：codeTop
计算机基础(上)（“八股”） 校招笔记（一）__Java_Java入门 C++后端后续更新
校招笔记（一）__Java_面对对象
校招笔记（一）__Java_集合
校招笔记（一）__Java_多线程
校招笔记（一）__Java_锁
校招笔记（一）__Java_JVM
计算机基础(下)（“八股”） 校招笔记（二）__计算机基础_Linux&Git
校招笔记（三）__计算机基础_计算机网络
校招笔记（四）__计算机基础_操作系统
校招笔记（五）__计算机基础_MySQL
校招笔记（六）__计算机基础_Redis
校招笔记（七）__计算机基础_数据结构
校招笔记（八）__计算机基础_场景&智力题
校招笔记（九）__计算机基础_相关补充
项目&实习 主要是怎么准备项目，后续更新

七、数据结构和算法

1. 如何对快排进行优化？

  • 三数取中法和随机交换法

    快排将选取的基准点经过调整放到合适的位置，之后将这个基准点左右两边的区间分别递归的进行快排。

    如果基准点的数据比较小，将会导致调整后基准点处于靠近两侧的位置，那么两边的区间长度将会严重失去平衡.

    三数取中法：指的是选取基准点之前我们可以拿出数列中间位置元素的值，将它和首尾的元素进行比较，之后将这三个数中的中间数交换到数列首位的位置，之后将这个数作为基准点，尽量减小之后的分区后左右两边的区间长度之差。

  • 三路分割法

    三路法同样是针对含有大量【重复数列】的优化。

    3路法的思想是将数列分成3个区间，分别是小于、等于和大于基准点的区间。那么分区之后，对于等于基准点的区间内的元素，我们就不需要对其做任何处理了，只需要递归的处理小于和大于基准点的元素即可。

  • 结合插入排序

    当待排序序列的长度分割到一定大小后，使用插入排序。

    • 对于很小和部分有序的数组，快排不如插排好。当待排序序列的长度分割到一定大小后，继续分割的效率比插入排序要差，此时可以使用插排而不是快排。

2.快排和堆排的区别？什么时候使用快排和堆排？

  • 快排和堆排区别？

    • 综合性能：实际应用中，虽然堆排序的时间复杂度要比快速排序稳定（快排最差退化成O(N^2)） ，但是统计意义上这种情况较少，所以综合性能还是快排更优；

    • 交换次数： 对于同样的数据，在排序过程中，堆排序算法的数据交换次数要多于快速排序；

    • 访问友好： 堆排序数据访问的方式没有快速排序友好。

      对于快速排序来说，数据是顺序访问的；而堆排序来说，数据是跳着访问的。比如，堆排序中，最重要的一个操作就是数据的堆化。对堆顶节点进行堆化，会一次访问数组下标1，2，4，8的元素，而不是像快排那样，局部顺序访问，所以对CPU缓存是不友好的。

  • 快排和堆排使用场景？

    • 快排： 绝大多数场合。

    • 堆排： topK问题、优先队列（需要在一组不停更新的数据中不停地找最大/小元素）

      在N个元素中找到top K，时间复杂度是O(N log K)，空间复杂的是O(K)，而快速排序的空间复杂度是O(N)。

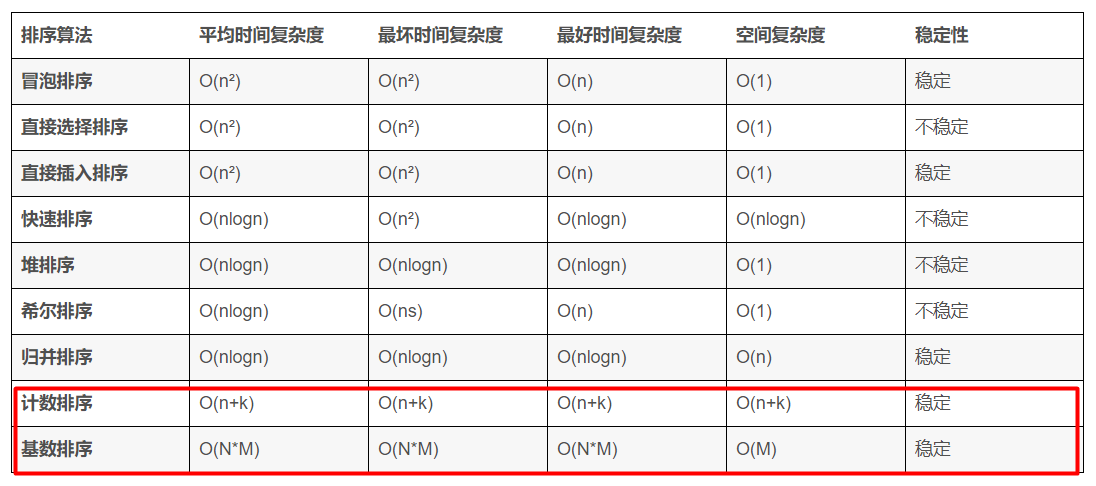
3. 【面试重点】有哪些排序算法，各算法的时间复杂度 ? 哪些是稳定的？为什么是稳定的？

image-20210501224258097

3.1 如果数据大致有序的，用什么排序比较好？

如果是大致有序，用 插入排序 比较好：

  • 直接插入排序是将第i个元素插入到已经排序好的前i-1个元素中 ，当元素基本有序时。和前i-1个元素末尾比较一次就可以直接插入。

在相比使用其它排序：

  • 归并排序： 归并排序和数组是否有序无关，都是O(nlgn)。

    归并排序是把一个有n个记录的无序文件看成由n个长度为1的有序子文件组成的文件，然后进行两两归并，得到[n/2]个长度为2或1的有序文件，再两两归并 。

  • 快速排序： 数组基本有序时，此时如果使用基点是最后一个元素，划分的两个子数组极为不平衡，每次划分比较次数都很多。所以不推荐。

4. 二叉查找树，红黑树和平衡二叉树的区别？（有了二叉查找树、平衡树（AVL）为啥还需要红黑树？）

总结来说：平衡树是为了解决二叉查找树退化为链表的情况；而红黑树是为了解决平衡树在插入、删除等操作需要频繁调整的情况。

  • 二叉查找树退化成单链表

    正常使用二叉查找树是类似于二分查找 O（logn），但是极端情况：

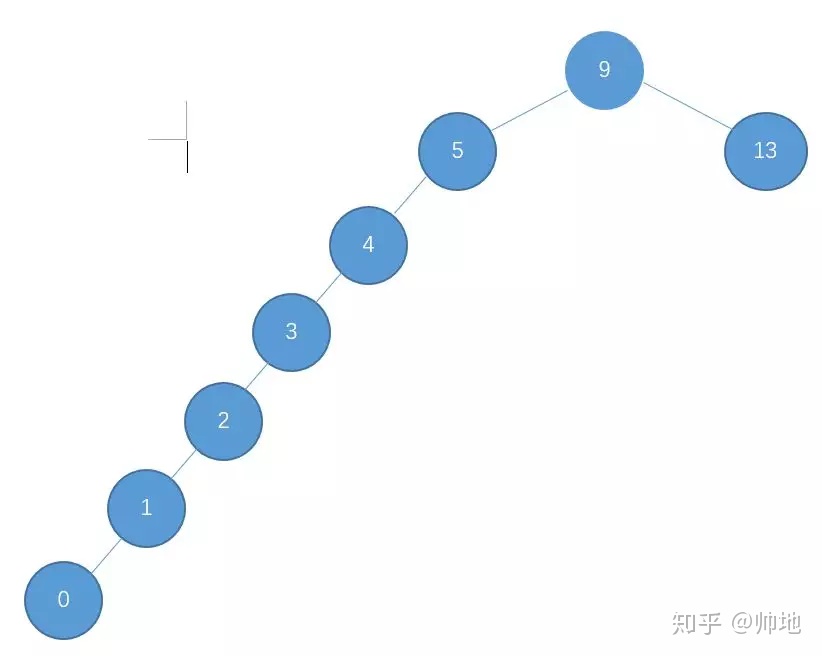
    • 构建的二叉树所有节点都只有右子树或左子树，此时时间复杂度退化成O(N)

      preview

  • 平衡二叉树频繁左右旋

    平衡二叉树就是为了解决二叉查找树退化成一颗链表而诞生了，平衡树具有如下特点：

    1. 具有二叉查找树的全部特性；

    2. 每个节点的左子树和右子树的高度差至多等于1。

    避免了二叉查找树极端情况产生，但是：

    • 每次进行插入/删除节点的时候，几乎都会破坏平衡树的第二个规则，进而我们都需要通过左旋和右旋来进行调整，使之再次成为一颗符合要求的平衡树。

    平衡树性能大打折扣。

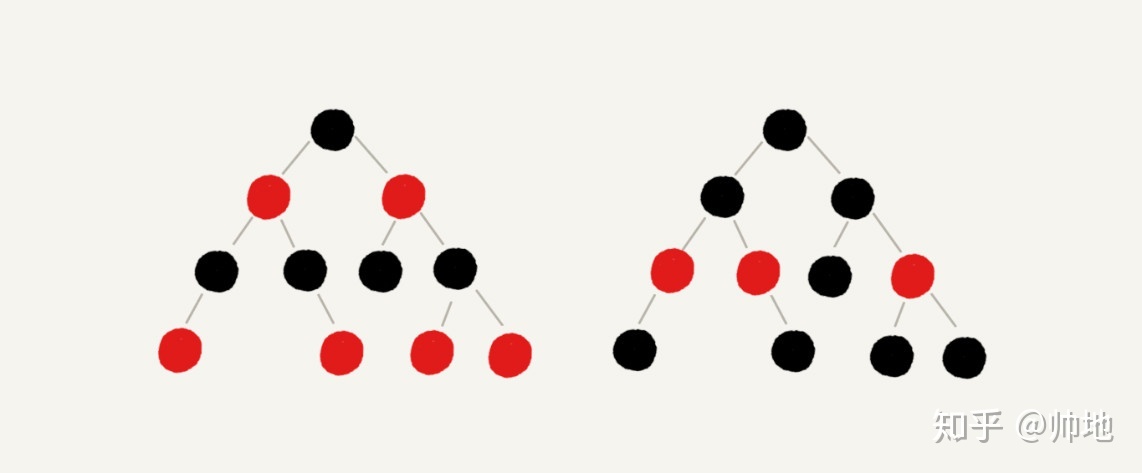
  • 红黑树规不需要频繁着调整

    红黑树具有如下特点：

    最坏情况下，也能在 O(logn) 的时间复杂度查找到某个节点。

    • 与平衡树不同的是，红黑树在插入、删除等操作，（🚩*1）不会像平衡树那样，频繁着破坏红黑树的规则，所以不需要频繁着调整，这也是我们为什么大多数情况下使用红黑树的原因；
    • 但是，单单在查找方面的效率的话，平衡树比红黑树快。

    img

    1. 具有二叉查找树的特点；
    2. 根节点是黑色的；
    3. 每个叶子节点都是黑色的空节点（NIL），也就是说，叶子节点不存数据；
    4. 任何相邻的节点都不能同时为红色，也就是说，红色节点是被黑色节点隔开的；
    5. 每个节点，从该节点到达其可达的叶子节点是所有路径，都包含相同数目的黑色节点。
4.1 为什么红黑树不需要频繁调整？

详细理解红黑树一篇不错的文章：百图详解红黑树，想不理解都难

平衡二叉树这种高度差为 1 的要求太严格了，尤其是对于频繁删除、插入的场景非常浪费时间。

但是由于红黑树：

  • 具有二叉树所有特点。
  • 每个节点只能是红色或者是黑色。
  • 根节点只能是黑色，且黑色根节点不存储数据。
  • 任何相邻的节点都不能同时为红色。
  • 红色的节点，它的子节点只能是黑色。
  • 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

不追求插入、删除等操作绝对平衡，只需满足上述条件即可。它的旋转次数少，插入最多两次旋转，删除最多三次旋转。

所以在搜索、插入、删除操作较多的情况下，红黑树的效率是优于平衡二叉树的。

5.快速排序的过程 ？

  • 手撕一个二分查找 和快排？

    • 二分查找

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      // binary search
          public int binarySearch(int[] arr, int value)
          {
              int left = 0,right = arr.length-1;
              int mid ;
              while (left<=right) //*<= 而不是< 
              {
                  mid = (left+right)/2;
                  if(value == arr[mid])
                  {
                      return mid; // 如果数组存在待查找元素，按照逻辑一定会是mid
                  }
                  else  if(value < arr[mid])
                  {

                      right = mid-1;
                  }
                  else  // value > arr[mid]
                  {
                      left = mid+1;
                  }

              }
              return -1;
          }

    • 快速排序

      1
      2
      3
      4
      5
      6
      7
      8
      9
      10
      11
      12
      13
      14
      15
      16
      17
      18
      19
      20
      21
      22
      23
      24
      25
      26
      27
      public int[] quick_sort(int[] arr,int left,int right)
          {
              if(right<=left){return null;}

              // 选择基准：数组最右数字
              // *如果选择最左，思考交换过程
              // *partition 左侧始终是比pivot小的数
              int pivot = arr[right];
              int partition = left;
              // 遍历分区元素
              // 小于基准的放基准左边，大于的放基准右边
              // * 终止条件：i < right 而非 right-1！
              for(int i=left; i< right;i++)
              {
                  if(arr[i]<pivot) // 实际只交换小于到左边即可
                  {
                      swap(arr,i,partition);
                      partition++;
                  }
              }
              // *基准插入位置partition位置
              swap(arr,partition,right);
              //递归的排序
              quick_sort(arr,left,partition-1);
              quick_sort(arr,partition+1,right);
              return arr;
          }

6. 布隆过滤器原理？为什么使用多个哈希函数？其它相关应用？

参考：详解布隆过滤器的原理，使用场景和注意事项

“布隆说：不存在的那么一定不存在”

“布隆说：存在的那么只是可能存在”

7.1 从HashMap说起—当你判断某个元素时候你在想什么？

通常我们怎么判断一个数组，是否存在某个元素呢？

聪明的你一定想到HashMap：（1）HashMap将数组所有元素使用哈希函数，映射到HashMap上（HashMap本身也是一个数组）（2）然后就可以在O(1)级别判断某个元素是否存在。

但是这种做法通常会导致以下问题：

  1. 一旦数组很大，比如上亿，HashMap将会占据非常大的内存；
  2. 数组很大，不大可能一次性能在内存构建HashMap；
  3. 而且HashMap，通常存在负载因子，是不能充分利用内存的。

为此，我们可以从以下方向优化：

  • 只存储key。但是，因为我们只要判断某个元素（key）是否存在， 不需要取出对应key的value—也就是不需要存储value。

  • key映射为bit数组索引。key映射为bit数组索引，即位图对应索引， 索引对应数值用 0/1 就可以标识为是否存在该key。

为此，我们可以【第一阶段优化】如下：

img

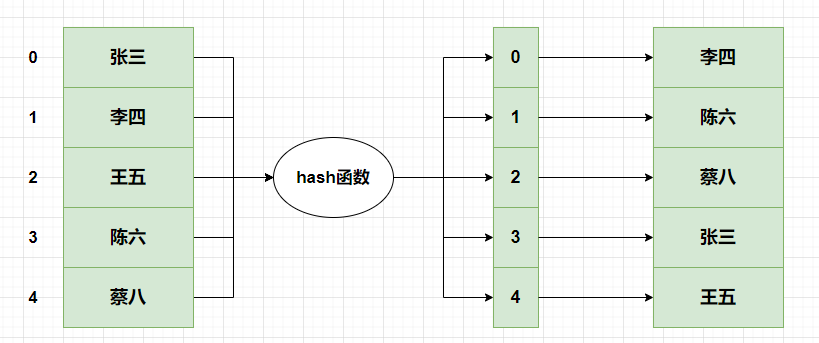
看样子似乎是满足我们要求了，但是依旧存在以下问题：

  1. 只使用一个hash函数，空间利用率低。

一个hash函数只能将key散列到一个位置 ，虽然hash尽量优良映射均匀，但是空间利用率依然不算高。

因此，我们可以多个函数，将key同时映射到多个位置，即使发生哈希冲突，某个位置被覆盖，其它依旧存在，变相的降低了哈希冲突。

7.2 数据结构及原理

布隆过滤器，最终结构如下：一个bit数组，采用多个hash函数进行映射。

img

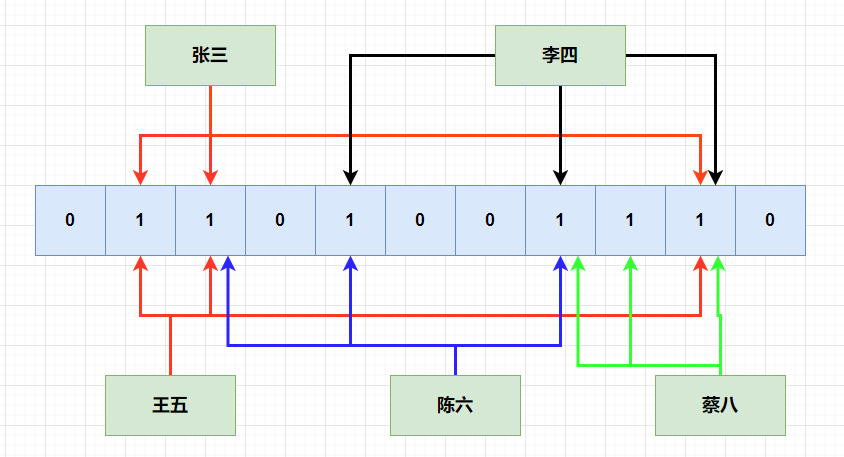
7.3 布隆函数优缺点
  • 优点
    1. 存储/插入/查询时间复杂度，都是常数级别O(1)
    2. 保密性好，因为不需要存储数据本身
    3. 存储数据大，可以存储非常大的数据本身
  • 缺点
    1. 随着元素数量增加，误算率会增加
    2. 不能删除元素，因为删除某个元素，要把其对应所有hash函数散列的位置如A,B，置为0 。其它元素的可能散列到位置A，再去判断这个元素是否存在就会出现误判。
7.4 应用场景

  1. 解决缓存穿透，防止不存在的元素去查询数据库

  2. 防止重复被攻击，用户第一次请求，将请求参数放入布隆过滤器中，当第二次请求时，先判断请求参数是否被布隆过滤器命中。可以提高缓存命中率

  3. 判断用户是否阅读过某视频或文章， 比如抖音或头条，当然会导致一定的误判，但不会让用户看到重复的内容。